Bi-directional Attention Flow for Machine Comprehension
Overview
- The motivation is that attention should flow both ways (from context to question and from question to context).
Architecture
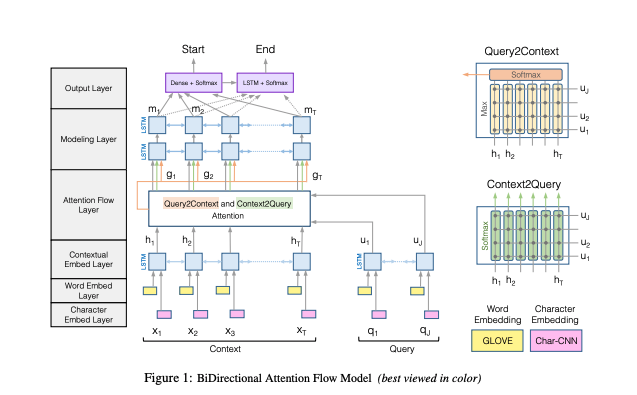
- The core idea behind the paper is on the Bi-directional attention layer between the context (decoder) and the question (encoder).
Assume we’ve the context hidden states \(c_1,....,c_N \in \mathbb{R}^{2h}\) and question hidden states \(q_1,....,q_M \in \mathbb{R}^{2h}\). We compute the similarity matrix S \(\in \mathbb{R}^{NxM}\) which contains a similarity score Sij for each pair of (ci, qj) where
\[\begin{align*} S_{ij} = {w^T}_{sim} [c_i; q_j; c_i \circ q_j] \in \mathbb{R} \end{align*}\]where \(w_{sim}\) is a weight matrix of shape \(\mathbb{R}^{6h}\) and \(S \in \mathbb{R}^{NxM}\).
Context-to-Question Attention (C2Q)
We take a row-wise softmax of S to obtain the attention distributions \(\alpha^i\) which is used to take a weighted sum of the quesiton hidden states \(q_j\) yielding C2Q attention output a_i.
\[\begin{align*} \alpha^i = softmax(S_i;) \in \mathbb{R}^M \end{align*}\] \[\begin{align*} a_i = \sigma_{j=1}^{M} \alpha_j^iq_j \in \mathbb{R}^2h \end{align*}\]This is very similar to the normal attention (instead of dot-product we use the matrix similarity S). The intution is that for every word in context, we compute the similarity to every other word in question. We then take a softmax on top of this to get a weighted sum of the question hidden states. We do this for every word/token in context.
Question-To-Context Attention (Q2C)
Similarly, we take a column-wise softmax of S to obtain the attention distributions \(\beta\) which is used to take a weighted sum of the context hidden states \(c_i\) yielding C2Q attention output \(c'\).
Bi-directional Attention Flow
\[\begin{align*} b_i = [c_i; a_i; c_i \circ a_i; c_i \circ c' ] \end{align*}\]The intuition is that, for every word in context, we find the most similar word to question and then take a softmax of that to get a weight for every word in context. Now we take a weighted sum of the context hidden states to get \(c'\).
Results
| Paper | EM | F1 |
|---|---|---|
| Dynamic Co-attention Networks | 66.2 | 75.9 |
| BiDaf | 67.7 | 77.3 |
| No char embedding | 65 | 74.4 |
| No C2Q Attention | 57.2 | 67.7 |
| No Q2C Attention | 63.6 | 73.7 |
Kaushik Rangadurai
Code. Learn. Explore
